Rotate 3D vector to same orientation as another 3D vector - Rodrigues' rotation formula

I had a normal that I wanted to orient in a particular way, so I wanted to find the rotation necessary to orient the normal. Help from the Llama and some Googling brought me to this post at Math StackExchange and the Rodrigues' Rotation Formula.

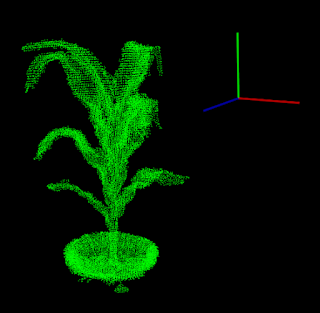
As for background, I had a point cloud that I wanted to align to the Z axis. Since the pot of the potted plant is a relatively constant feature in these images, I wanted to use the pot to orient the rest of the cloud.

I segmented a circle out to get the border of the pot. Here's the segmented circle, floating out in space.

In the context of the Stack Exchange post, I had a normal corresponding to a point in the center of the circle that I wanted to rotate to orient with the Z-axis (0, 0, 1). Between the Stack Exchange post, Wikipedia, and the Llama, I was able to write an implementation without actually knowing anything about linear algebra (see below). Everything appears to work just fine (the cyan circle is after transformation).

This implementation uses the Eigen library and the PCL library. The nomenclature is similar to the Stack Exchange post.

// This is an implementation of Rodrigues' Rotation Formula
// https://en.wikipedia.org/wiki/Rodrigues'_rotation_formula
// Following http://math.stackexchange.com/questions/293116/rotating-one-3-vector-to-another?rq=1
// Problem: Given two 3-vectors, A and B, find the rotation of A so that its orientation matches B.
// There are some edge cases where this implementation will fail, notably if the norm of the cross product = 0.

// Step 1: Find axis (X)
Eigen::Vector3f crossProduct = vector_A.cross(vector_B);
float crossProductNorm = crossProduct.norm();
Eigen::Vector3f vector_X = (crossProduct / crossProductNorm);

// Step 2: Find angle (theta)
float dotProduct = vector_A.dot(vector_B);
float norm_A = vector_A.norm();
float norm_B = vector_B.norm();
float dotProductOfNorms = norm_A * norm_B;
float dotProductDividedByDotProductOfNorms = (dotProduct / dotProductOfNorms);
float thetaAngleRad = acos(dotProductDividedByDotProductOfNorms);

// Step 3: Construct A, the skew-symmetric matrix corresponding to X
Eigen::Matrix3f matrix_A = Eigen::Matrix3f::Identity();

matrix_A(0,0) = 0.0;
matrix_A(0,1) = -1.0 * (vector_X(2));
matrix_A(0,2) = vector_X(1);
matrix_A(1,0) = vector_X(2);
matrix_A(1,1) = 0.0;
matrix_A(1,2) = -1.0 * (vector_X(0));
matrix_A(2,0) = -1.0 * (vector_X(1));
matrix_A(2,1) = vector_X(0);
matrix_A(2,2) = 0.0;

// Step 4: Plug and chug.
Eigen::Matrix3f IdentityMat = Eigen::Matrix3f::Identity();
Eigen::Matrix3f firstTerm = sin(thetaAngleRad) * matrix_A;
Eigen::Matrix3f secondTerm = (1.0 - cos(thetaAngleRad)) * matrix_A * matrix_A;

Eigen::Matrix3f matrix_R = IdentityMat + firstTerm + secondTerm;

// This is the rotation matrix. Finished with the Rodrigues' Rotation Formula implementation.
std::cout << "matrix_R" << std::endl << matrix_R << std::endl;


// We copy the rotation matrix into the matrix that will be used for the transformation.
Eigen::Matrix4f Transform = Eigen::Matrix4f::Identity();
Transform(0,0) = matrix_R(0,0);
Transform(0,1) = matrix_R(0,1);
Transform(0,2) = matrix_R(0,2);
Transform(1,0) = matrix_R(1,0);
Transform(1,1) = matrix_R(1,1);
Transform(1,2) = matrix_R(1,2);
Transform(2,0) = matrix_R(2,0);
Transform(2,1) = matrix_R(2,1);
Transform(2,2) = matrix_R(2,2);

// Now that we have the rotation matrix, we can use it to also find the translation to move the cloud to the origin.
// First, rotate a point of interest to the new location.
Eigen::Vector3f modelVectorAxisPointTransformed =  matrix_R * modelVectorAxisPoint;

// Add the translation to the matrix.
Transform(0,3) = modelVectorAxisPointTransformed(0) * (-1.0);
Transform(1,3) = modelVectorAxisPointTransformed(1) * (-1.0);
Transform(2,3) = modelVectorAxisPointTransformed(2) * (-1.0);

// Perform the transformation
pcl::transformPointCloud(*cloudPot, *cloudPotTransformed, Transform);

And finally, an image showing all the viewports.